在C++中实现高效的数组原地轮转的方法总结
41人参与 • 2025-04-12 • C/C++
一、问题: 数组轮转
给定一个长度为 n 的整数数组 nums,请将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例:
输入:nums = [1, 2, 3, 4, 5, 6, 7], k = 3 输出:[5, 6, 7, 1, 2, 3, 4] 解释: 向右轮转 1 步:[7, 1, 2, 3, 4, 5, 6] 向右轮转 2 步:[6, 7, 1, 2, 3, 4, 5] 向右轮转 3 步:[5, 6, 7, 1, 2, 3, 4]
要求:
- 实现数组的右轮转功能。
- 尽可能探索多种解决方案。 至少思考三种不同的算法思路。
- 挑战: 能否设计一个 空间复杂度为 o(1) 的原地算法 来解决此问题? 尝试优化解决方案,使其具有尽可能高的效率。
- 分析提出的每种解决方案的时间复杂度和空间复杂度。
提示:
- 考虑
k大于数组长度n的情况。 - 仔细思考数组轮转的本质,尝试从不同的角度分解问题。

二、问题分析
数组轮转的本质是将数组中的元素整体向右移动 k 个位置,超出数组边界的元素会“循环”回到数组的开头。
关键点:
- k 的有效性: 当
k大于等于数组长度n时,实际轮转的步数是k % n。 例如,如果n = 7,k = 9,那么实际轮转 2 步。 因此,需要对k进行取模运算。 - 实现空间复杂度为 o(1) 的原地算法是难点。 这意味着不能使用额外的数组来存储临时结果。
- 效率: 如何尽可能减少元素移动的次数,提高算法效率。
思路 1: 暴力法(重复移动)。
- 将数组的最后一个元素移动到第一个位置,其他元素依次向右移动。
- 重复这个过程
k次。 - 优点: 实现简单,容易理解。
- 缺点: 时间复杂度高,效率低,为 o(n * k)。 当 k 接近 n 时,效率非常差。
思路 2: 使用额外数组。
- 创建一个新的数组
new_nums,长度与原数组相同。 - 将原数组
nums中的每个元素nums[i]放到新数组的new_nums[(i + k) % n]位置上。 - 将新数组
new_nums复制回原数组nums。 - 优点: 时间复杂度较低,为 o(n)。
- 缺点: 需要额外的 o(n) 空间,不满足原地算法的要求。
思路 3: 反转数组。
- 将整个数组反转。
- 将数组的前
k % n个元素反转。 - 将数组的后
n - (k % n)个元素反转。 - 原理:
- 例如
nums = [1, 2, 3, 4, 5, 6, 7], k = 3 - 反转整个数组:
[7, 6, 5, 4, 3, 2, 1] - 反转前 k 个元素:
[5, 6, 7, 4, 3, 2, 1] - 反转后 n-k 个元素:
[5, 6, 7, 1, 2, 3, 4]
- 例如
- 优点: 时间复杂度为 o(n),空间复杂度为 o(1),满足原地算法的要求。
- 缺点: 需要对数组进行三次反转操作,理解起来稍微复杂一些。
思路 4: 循环替换。
- 从位置 0 开始,将该位置的元素移动到
(0 + k) % n位置,再将该位置的元素移动到(0 + 2k) % n位置,以此类推。 - 为了避免重复循环,需要记录已经访问过的位置,或者使用一个计数器来控制循环的次数。
- 优点: 空间复杂度为 o(1)。
- 缺点: 实现相对复杂,需要仔细处理循环的边界条件。时间复杂度o(n)。
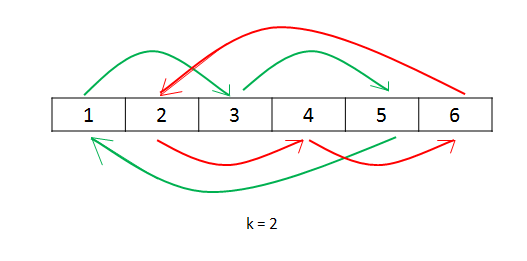
思路 5: 使用gcd(最大公约数)来优化循环替换。
如果
n和k的最大公约数是 1,那么只需要一个循环就能完成所有的替换。 但如果最大公约数不是1,则需要多个循环。找到
n和k的最大公约数gcd。 循环从0到gcd - 1。 在每个循环中,执行循环替换。优点: 优化了循环替换算法
缺点: 需要计算最大公约数,复杂度增加。
复杂度分析:
| 解决方案 | 时间复杂度 | 空间复杂度 | 原地算法? |
|---|---|---|---|
| 暴力法 | o(n * k) | o(1) | 是 |
| 额外数组 | o(n) | o(n) | 否 |
| 反转数组 | o(n) | o(1) | 是 |
| 循环替换 | o(n) | o(1) | 是 |
| gcd循环替换 | o(n) | o(1) | 是 |
三、算法实现
3.1、使用额外数组(效果较差)
- 创建一个新的数组
new_nums,长度与原数组相同。 - 将原数组
nums中的后k % num.size()个元素nums[i]放到新数组的开头位置上,其他元素依次放在末尾。 - 将新数组
new_nums复制回原数组nums。
class solution {
public:
void rotate(vector<int>& nums, int k) {
unsigned n = k % nums.size();
if (n == 0)
return;
vector<int> ret(nums.end() - n, nums.end());
for (unsigned i = 0; i < (nums.size() - n); ++i)
ret.emplace_back(nums[i]);
std::swap(ret, nums);
}
};
时间复杂度:
- 时间复杂度较低,为 o(n)。
- 需要额外的 o(n) 空间。
3.2、反转数组3次(实现简单)
这种方法实现相对容易,而且容易理解。
- 将整个数组反转。
- 将数组的前
k % n个元素反转。 - 将数组的后
n - (k % n)个元素反转。
原理:
- 例如
nums = [1, 2, 3, 4, 5, 6, 7], k = 3 - 反转整个数组:
[7, 6, 5, 4, 3, 2, 1] - 反转前 k 个元素:
[5, 6, 7, 4, 3, 2, 1] - 反转后 n-k 个元素:
[5, 6, 7, 1, 2, 3, 4]
代码实现:
class solution {
public:
void rotate(vector<int>& nums, int k) {
unsigned n = k % nums.size();
if (n == 0)
return;
unsigned size = nums.size();
for (unsigned i = 0; i < size / 2; ++i)
std::swap(nums[i], nums[size - i - 1]);
for (unsigned i = 0; i < n / 2; ++i)
std::swap(nums[i], nums[n - i -1]);
for (unsigned i = 0; i < (size - n) / 2; ++i)
std::swap(nums[i + n], nums[size - i - 1]);
}
};
3.3、循环替换(较为复杂)
从位置 0 开始,将该位置的元素移动到 (0 + k) % n 位置,再将该位置的元素移动到 (0 + 2k) % n 位置,以此类推。
为了避免重复循环,需要记录已经访问过的位置,或者使用一个计数器来控制循环的次数。
可以使用gcd(最大公约数)来优化循环替换:
如果
n和k的最大公约数是 1,那么只需要一个循环就能完成所有的替换。 但如果最大公约数不是1,则需要多个循环。找到
n和k的最大公约数gcd。 循环从0到gcd - 1。 在每个循环中,执行循环替换。
class solution {
public:
void rotate(vector<int>& nums, int k) {
unsigned n = nums.size();
int gcd = std::gcd(n, k % n);
for (int i = 0; i < gcd; ++i) {
int cur = i;
int pre = nums[cur];
do {
int next = (cur + k) % n;
std::swap(nums[next], pre);
cur = next;
} while (cur != i);
}
}
};
四、总结
c++中数组轮转问题的五种解决方案:暴力法、额外数组、反转数组、循环替换以及gcd优化循环替换。分析了每种算法的时间和空间复杂度,并特别关注了原地算法的实现。通过对比不同方案,展示了如何在时间和空间之间权衡,最终实现高效且节省空间的数组轮转。
其中,反转数组和gcd优化循环替换是在实际项目中推荐使用的。
以上就是在c++中实现高效的数组原地轮转的方法总结的详细内容,更多关于c++数组原地轮转的资料请关注代码网其它相关文章!
 微信扫一扫
微信扫一扫
您想发表意见!!点此发布评论






发表评论