LSTM（长短期记忆神经网络）_机器学习

一、什么是lstm

二、为什么更倾向于使用lstm？

最基础版本的rnn，我们可以看到，每一时刻的隐藏状态都不仅由该时刻的输入决定，还取决于上一时刻的隐藏层的值，如果一个句子很长，到句子末尾时，它将记不住这个句子的开头的内容详细内容

个例子来说明这个问题：

假设我们有一个简单的rnn用于生成文本，下面是一个包含长句子的例子：

"the cat sat on the mat. it was fluffy and had a long tail. in the corner of the room, a little mouse peeked out."

在训练rnn时，模型会逐个时间步处理每个单词。当模型处理到句子的末尾时，它的隐藏状态包含了整个句子的信息。然而，由于梯度消失的问题，模型可能在处理过程中忘记了句子开头的重要信息。

例如，在处理"peeked out"这个短语时，如果模型已经遗忘了"the cat sat on the mat."的信息，那么它可能无法正确理解"peeked out"的上下文，因为它缺乏前文的语境。

这就是为什么在处理长序列时，特别是在自然语言处理等任务中，更先进的模型如长短时记忆网络（lstm）和门控循环单元（gru）等被提出来，以解决rnn的梯度问题，更好地捕捉长期依赖关系。这些模型通过引入门控机制来控制信息的流动，从而提高了对长序列的建模能力。

三、lstm的结构与普通rnn有何不同

lstm是rnn的一种变体，更高级的rnn，那么它的本质还是一样的，还记得rnn的特点吗，可以有效的处理序列数据，当然lstm也可以，还记得rnn是如何处理有效数据的吗，是不是每个时刻都会把隐藏层的值存下来，到下一时刻的时候再拿出来用，这样就保证了，每一时刻含有上一时刻的信息，如图，我们把存每一时刻信息的地方叫做memory cell，中文就是记忆细胞，可以这么理解。

lstm和普通rnn的区别在于rnn什么信息它都存下来，因为它没有挑选的能力，而lstm不一样，它会选择性的存储信息，因为它能力强，它有门控装置，它可以尽情的选择。如下图，普通rnn只有中间的memory cell用来存所有的信息，而从下图我们可以看到，lstm多了三个gate，也就是三个门，什么意思呢？在现实生活中，门就是用来控制进出的，门关上了，你就进不去房子了，门打开你就能进去，同理，这里的门是用来控制每一时刻信息记忆与遗忘的。

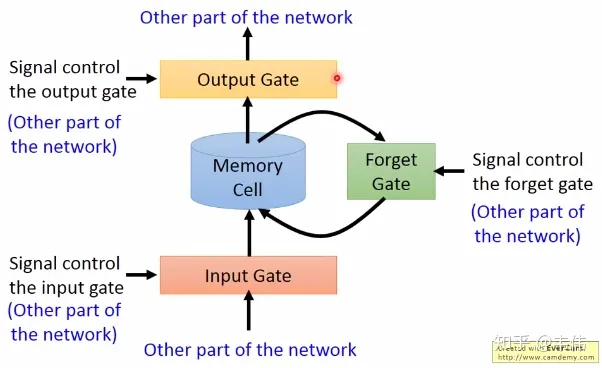
那么这三个门分别都是用来干什么的？

input gate：中文是输入门，在每一时刻从输入层输入的信息会首先经过输入门，输入门的开关会决定这一时刻是否会有信息输入到memory cell。
output gate：中文是输出门，每一时刻是否有信息从memory cell输出取决于这一道门。
forget gate：中文是遗忘门，每一时刻memory cell里的值都会经历一个是否被遗忘的过程，就是由该门控制的，如果打卡，那么将会把memory cell里的值清除，也就是遗忘掉。

那么我们就可以总结出这个过程：先经过输入门，看是否有信息输入，再判断遗忘门是否选择遗忘memory cell里的信息，最后再经过输出门，判断是否将这一时刻的信息进行输出。

下面来看一下lstm的内部结构把！！！

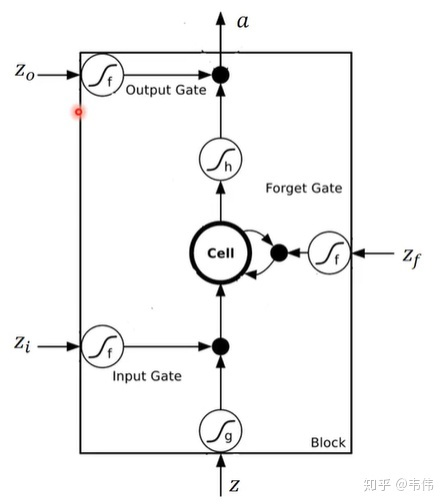
先来看一下这个符号：代表一个激活函数，lstm里常用的激活函数有两个，一个是tanh，一个是sigmoid。

然后通过下面的图来说明四个输入分别是什么

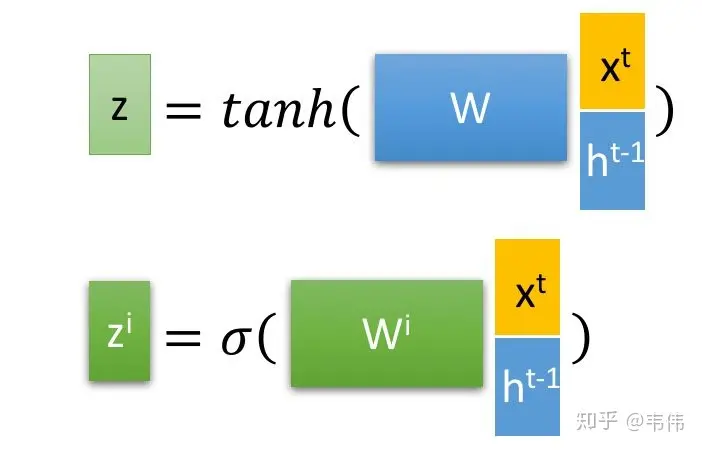
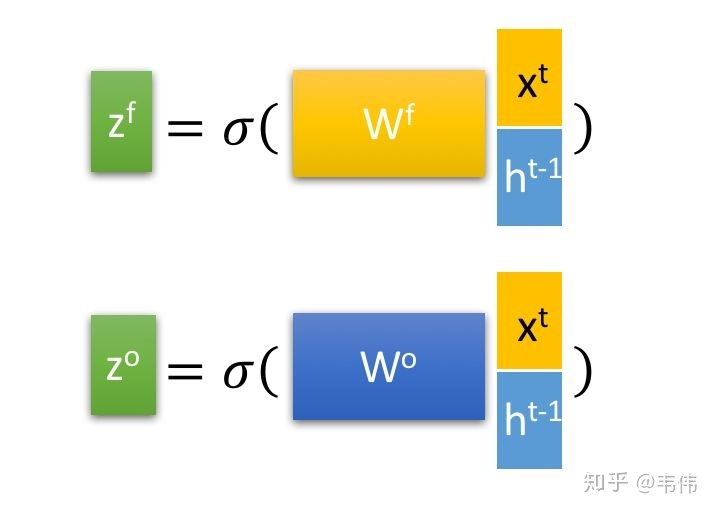
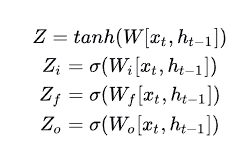
首先解释一下，经过这个sigmod激活函数后，得到的都是在0到1之间的数值，1表示该门完全打开，0表示该门完全关闭，

其中是最为普通的输入，可以从上图中看到，是通过该时刻的输入和上一时刻存在memory cell里的隐藏层信息向量拼接，再与权重参数向量点积，得到的值经过激活函数tanh最终会得到一个数值，也就是，注意只有的激活函数是tanh，因为是真正作为输入的，其他三个都是门控装置。

再来看，input gate的缩写i，所以也就是输入门的门控装置，同样也是通过该时刻的输入和上一时刻隐藏状态，也就是上一时刻存下来的信息向量拼接，在与权重参数向量点积（注意每个门的权重向量都不一样，这里的下标i代表input的意思，也就是输入门）。得到的值经过激活函数sigmoid的最终会得到一个0-1之间的一个数值，用来作为输入门的控制信号。