【kg推荐-＞精读】RippleNet: Propagating User Preferences on the Knowledge Graph for Recommender Systems

ripplenet

abstract

为了解决协同过滤的稀疏性和冷启动问题，通常利用side information，比如social networks，item attributes。

为了解决基于embedding和基于path的knowledge-aware recommendation的局限性，提出了ripplenet。ripple名为涟漪，模型通过自动地、迭代地延伸用户的潜在兴趣（沿着kg的links），促进 用户偏好在knowledge entities上的传播。因此，用户历史点击item的多个“ripples”（涟漪）被叠加，形成用户对候选item的偏好分布，用于预测最终点击的概率。

keywords

• recommender systems
• knowledge graph
• preference propagation

1 introduction

🔆基于kg的推荐的3个好处：

1. kg引入了item间的语义关系，有助于发现它们的潜在联系
2. kg由多种类型的关系组成，有助于扩展用户兴趣、增加推荐item的多样性
3. kg将用户的历史记录和推荐记录连接起来，为推荐带来可解释性

现有的kg分为2类：

• 基于embedding的方法[32,33,43]

使用knowledge graph embedding(kge) [35]预处理kg，并将学习到的entity embedding结合到推荐框架中去。例如dkn[33], cke[43], shine[32]。

这种方法灵活性高，但kge方法更适合in-graph应用，比如link prediction，而不是推荐[35]。

• 基于path的方法[42,45]

探索kg中items之间的各种连接模式，为推荐提供指导。例如per[42], meta-graph based recommendation[45]将kg视为异构信息网络（hin），并提取基于元路径/元图的潜在特征，以表示用户和项目之间沿着不同类型的关系路径/图的连通性。

这种方法更自然、直观，但是严重依赖手动设计的元路径，在实践中很难优化。或者说有些场景不可能手动设计元路径。

---

为了解决以上局限，提出了ripplenet

模型用于ctr预测，输入：user-item对；输出：user 点击(engaging) item的概率。

模型的关键思想：preference propagation。对于user，模型将他的历史兴趣作为kg中的seed set，然后 沿着kg的连接 迭代地 扩展用户的兴趣。，以发现他对于 候选item 的hierarchical potential interests（分层潜在兴趣）。

preference propagation与涟漪做类比，多个“涟漪”叠加，形成用户在kg上的最终偏好分布。

ripplenet的优点（结合了上述2种方法的优点）：

1. 使用kge方法用于preference propagation。
2. 从用户历史记录中的item到候选item，可以自动地发现可能路径，不需要手工设计。

2 problem formulation

user-item interaction mtrix y

knowledge graph $\mathcal{g}$，(h, r, t)三元组

问题描述：给定y和$\mathcal{g}$。

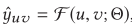
给定用户u，item v，$\theta$是函数参数，返回u是否点击v的概率。

3 ripplenet

3.1 framework

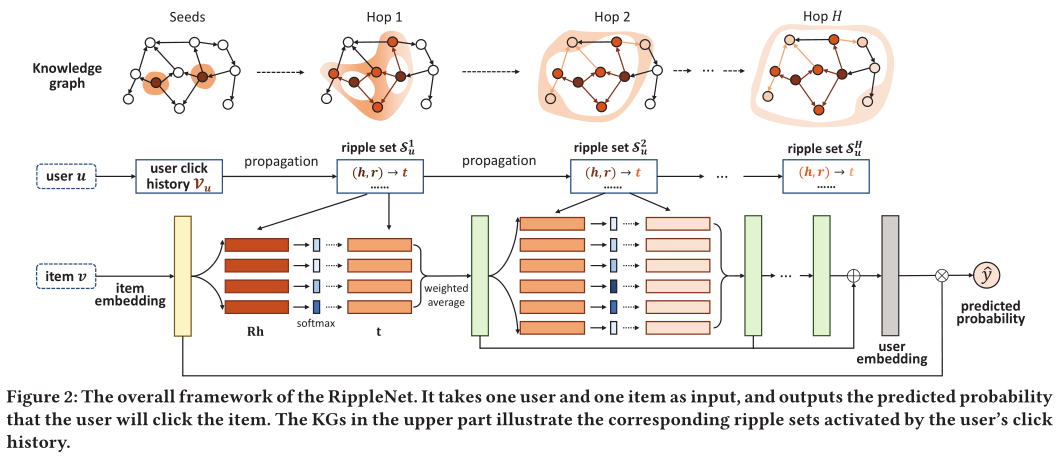
ripplenet框架如图2所示。输入：用户u，item v。输出：u点击v的预测概率。

对于输入用户u，他的历史兴趣集${\mathcal{v}}_u$作为kg的seeds，然后沿着link扩展，形成ripple sets ${\mathcal{s}}_u^k(k=1,2,...,h)$。ripple set ${\mathcal{s}}_u^k$是距离seed set ${\mathcal{v}}_u$ k-hop的set of knowledge triples。

ripple sets和item embedding（黄色块）迭代交互，以获得u对v的responses（绿色块），之后将其组合形成最终的user embedding（灰色块）。最后，使用u的embedding和v的embeddng，计算预测概率${\hat{y}}_{uv}$。

3.2 ripple set

kg可以让很多实体联系在一起，如图3所示。

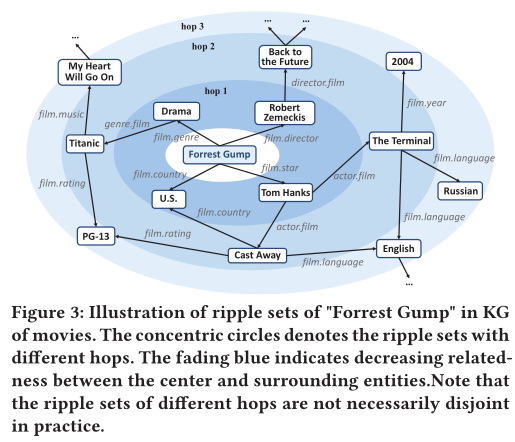
为了根据kg来描述用户的hierarchically extended preference（分层扩展偏好），ripplenet递归地定义了针对用户u的k-hop相关实体集，如下所示：

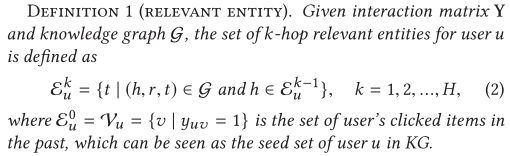
其中${\epsilon }_u^0$表示user点击过的item = seed set。（其实从图2就很好理解了）

模型借用“ripple”这个概念有两层含义：

1. 用户对item的潜在兴趣从历史偏好开始，从近到远逐层传播
2. 其强度随着跳数k的增加而减弱，如图3

还有一个关心的问题是，随着跳数k的增加，它们的大小可能会变得太大。如何解决？

1. kg中大量实体是汇入实体（sink entities），无outgoing links，比如“2004”、“pg-13”。
2. 我们还可以局限场景相关的类别，比如例子中只选择与firm相关的类别
3. 我们不会设置太大的最大跳数h，不然会带来很多噪声
4. 我们可以固定 邻居集的大小。

3.3 preference propagation

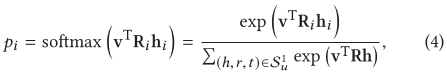
p i可以被视为在item v和 在关系r i空间中测量实体h i 的相似性。

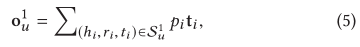
t i为tail的embedding；$o_u^1$看成对于item v的用户u历史记录${\mathcal{v}}_u$的1-order response。

通过等式4和5的操作，用户的兴趣沿着$s_u^1$中的links 从其历史集合${\mathcal{v}}_u$转移到set of 1-hop relevant entities ${\epsilon }_u^1$，这在ripplenet中称为preference propagation。

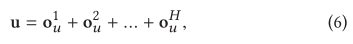
通过迭代执行，v替换为$o_u^1$，等等等等，就可以获得$s_u^i$，i=1, …, h。则user u对于item v的embedding是通过组合所有order来计算的。理论上讲最后一跳包含了以前跳的所有信息，但是还是要加起来，因为它们可能被稀释了。

最后，将用户embedding和项目embedding结合起来，以输出预测的点击概率。$\sigma (x)$是sigmoid函数。

3.4 learning algorithm

xxx（有关如何训练模型）

q1. 里面有用到贝叶斯定理，具体作用？

3.5 discussion

3.6 links to existing work

q2. 用到了很多另外的技术，比如attention，knowledge graph embedding，后面要学

• attention mechanism
• memory networks
• knowledge graph embedding

4 experiments

5 conclusion and future work

• 模型通过preference propagation，克服了基于embedding和path的局限性，自动传播用户的潜在偏好，探索kg中用户的分层兴趣。
• 在贝叶斯框架-点击率预测中，统一偏好传播 与 kge正则化。

我的疑问/总结

q1-q2

推荐理论视频：b站