数学建模6——路径规划的各种算法(Dijkstra、Floyd、A*、D*、RRT*、LPA*)

前言：本文只是简单的介绍一下各路径规划算法的概念和流程，可用于对算法的初步了解，如果要进一步学习，可以在个人理解中找到我推荐的其他博主更为完善的文章。

目录

一、dijkstra

基本概念

基本流程

个人理解

matlab代码

二、floyd

基本概念

基本流程

个人理解

matlab代码

三、a*算法

基本概念

基本流程

个人理解

matlab代码

四、d*算法

基本概念

基本流程

个人理解

matlab代码

五、rrt*算法

基本概念

基本流程

个人理解

六、lpa*算法

基本概念

基本流程

个人理解

七、d*lite算法

基本概念

基本流程

个人理解

八、各路径规划算法之间的区别（重要）

最后总结

一、dijkstra

基本概念

dijkstra算法是一种用于求解图中单源最短路径问题的经典算法。它可以用来找到从一个顶点到其他所有顶点的最短路径。

以下是dijkstra算法的基本概念：

1. 数据结构：dijkstra算法使用两个主要的数据结构来实现最短路径的计算（就是两个数据集）：
   1. 顶点集合：包含图中所有的顶点。
   2. 距离集合：记录从起点到每个顶点的最短路径距离。
2. 初始化：首先，将起点的距离设置为0，其他顶点的距离设置为无穷大。将起点设置为当前顶点。
3. 迭代更新：重复以下步骤，直到所有顶点都被标记为已访问。
   1. 选择当前顶点的邻居中距离最短的顶点，设为下一个当前顶点。
   2. 更新其他邻居的距离，如果通过当前顶点到达邻居的距离比当前记录的距离要短，则更新距离。
4. 标记顶点：在每次迭代更新后，将当前顶点标记为已访问，表示已经找到了从起点到该顶点的最短路径。
5. 最短路径提取：在所有顶点都被标记为已访问后，就可以提取出从起点到其他所有顶点的最短路径。

dijkstra算法的基本思想是通过不断更新距离集合中的距离，逐步找到最短路径。它保证每次迭代都会选择当前距离最短的顶点作为下一个当前顶点，并通过该顶点更新其他顶点的距离。最终，得到起点到其他所有顶点的最短路径和对应的距离。

基本流程

dijkstra算法的基本流程如下：

1. 创建一个距离集合和一个顶点集合。距离集合用于记录从起点到每个顶点的最短路径距离，初始时所有距离设置为无穷大（表示无法到达）。顶点集合用于存储图中的所有顶点。
2. 将起点的距离设置为0，并将其标记为当前顶点。
3. 迭代更新距离集合，直到所有顶点都被标记为已访问。 a. 遍历当前顶点的所有邻居顶点。 b. 对于每个邻居顶点，计算通过当前顶点到达该邻居顶点的距离，即当前顶点的距离加上从当前顶点到邻居顶点的边的权重。 c. 如果计算得到的距离小于距离集合中记录的距离，则更新距离集合中该邻居顶点的距离。 d. 重复步骤a到c，直到遍历完当前顶点的所有邻居顶点。
4. 将当前顶点标记为已访问，表示已经找到了从起点到该顶点的最短路径。
5. 选择下一个当前顶点：从未访问的顶点中选择距离最短的顶点作为下一个当前顶点。
6. 重复步骤3到5，直到所有顶点都被标记为已访问。
7. 最短路径提取：根据距离集合中记录的最短路径距离，可以回溯找到从起点到其他所有顶点的最短路径。

通过以上流程，dijkstra算法能够逐步更新距离集合中的距离，最终得到从起点到其他所有顶点的最短路径和对应的距离。

个人理解

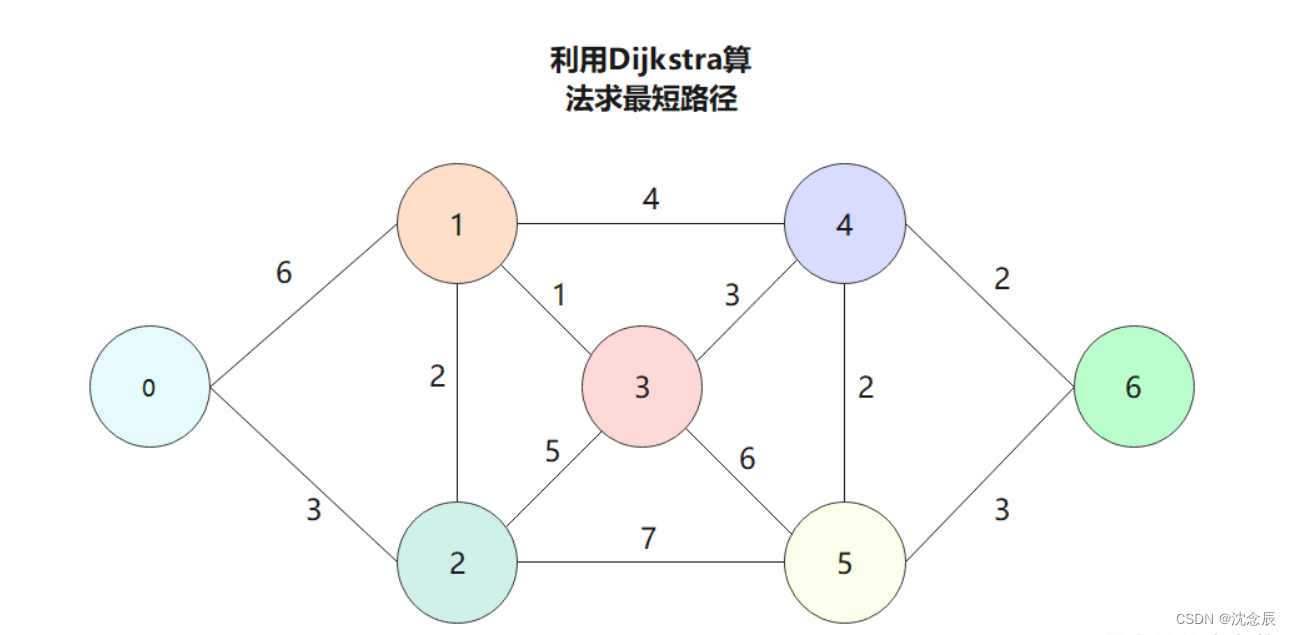
说白了就是问你：上面的图你怎么走可以把所有的点都走一遍，然后还需要路径长度最短。

这方法给出的答案是：我一个个点去摸索，比如我先从0到2最近，然后再从2开始摸索，发现接下来走1最好，因为0-2-1是5米，但0-2-3是8，0-2-5是10，然后我们确定0-2-1之后，再从1开始摸索，就这样慢慢找，最后找到最短路径。

具体学习可以参考这篇文章：图算法——求最短路径（dijkstra算法）​​​​​​​

matlab代码

%在这个代码中，首先定义了一个带权有向图的邻接矩阵，然后定义了起点和终点。接着，初始化到各个节点的距离、前驱节点和已访问状态。然后，运行dijkstra算法，找到最短路径和最短距离。最后，使用matlab的fprintf函数输出结果。
% 定义带权有向图
n = 5; % 节点数
adj_matrix = [0 10 0 5 0; 0 0 1 2 0; 0 0 0 0 4; 0 3 9 0 2; 7 0 6 0 0]; % 邻接矩阵

% 初始化
start_node = 1; % 起点
end_node = 5; % 终点
dist = inf(1, n); % 到各个节点的距离
prev = zeros(1, n); % 前驱节点
visited = zeros(1, n); % 是否已访问

dist(start_node) = 0;

% 运行dijkstra算法
for i = 1:n
    % 找到最近的未访问节点
    min_dist = inf;
    for j = 1:n
        if visited(j) == 0 && dist(j) < min_dist
            min_dist = dist(j);
            curr_node = j;
        end
    end
    
    % 更新距离和前驱节点
    visited(curr_node) = 1;
    for j = 1:n
        if adj_matrix(curr_node, j) > 0 && visited(j) == 0
            new_dist = dist(curr_node) + adj_matrix(curr_node, j);
            if new_dist < dist(j)
                dist(j) = new_dist;
                prev(j) = curr_node;
            end
        end
    end
end

% 输出结果
path = [end_node];
while path(1) ~= start_node
    path = [prev(path(1)), path];
end
fprintf('最短路径：');
fprintf('%d ', path);
fprintf('\n最短距离：%d\n', dist(end_node));

二、floyd

floyd算法又称为floyd-warshall算法，是一种动态规划算法，用于解决任意两点之间的最短路径问题。该算法在图中存在负权边和环的情况下仍然保证正确性。

floyd算法的思想是动态规划，通过枚举所有可能的中间节点，来逐步更新每个节点之间的距离。具体而言，算法根据当前结点之间的最短路径和中间节点更新后的最短路径，依次更新每个节点之间的最短路径。由于每次先将中间节点作为当前节点进行考虑，再按照不同的中间节点进行循环，所以也被称为多源最短路径算法。

基本概念

1. 初始化：
   1. 对于每对节点之间的边，设置其距离为边上的权值。
   2. 对于不存在直接相连的节点，其距离设置为无穷大（或者一个较大的数）。
   3. 对角线上的元素距离均为0。
2. 枚举中间节点：
   1. 对于图中的每个节点，假设其为中间节点。即以该节点为“中转站”，更新每对节点之间的距离。
   2. 对于每一对节点i,j，若它们的距离经过中间节点k比原先更优，则更新它们之间的距离为经过节点k的距离。
3. 重复迭代，直到所有节点之间的最短路径都求出：
   1. 如果所有节点都已经被遍历，算法终止。
   2. 否则，返回第2步，继续选择下一个中间节点进行更新。
4. 最短路径获取：
   1. 当所有节点之间的最短路径都求出后，就可以根据floyd算法矩阵中的数据来获取起始节点到每个节点的最短路径。
5. floyd算法的时间复杂度为o(n^3)，虽然有一定的计算量，但该算法相对于其他单源最短路径算法处理任意两点之间的最短路径问题十分高效。

基本流程

1. 创建一个二维数组d，用于存储任意两点之间的最短路径长度。初始时，d[i][j]表示顶点i到顶点j的边的权重，如果i和j之间没有边相连，则d[i][j]为无穷大。
2. 通过枚举中间节点k，逐步更新d数组中的元素。即，对于所有的i和j，若d[i][j] > d[i][k] + d[k][j]，则更新d[i][j]为d[i][k] + d[k][j]。
3. 重复步骤2，直到枚举完所有的中间节点k。
4. 最终得到的d数组即为任意两点之间的最短路径长度。

值得注意的是，在floyd算法中，对于每个中间节点k，都会更新一次所有顶点之间的距离，时间复杂度为o(n^3)。因此，floyd算法适用于顶点数较少的图，对于大型图来说效率较低。

个人理解

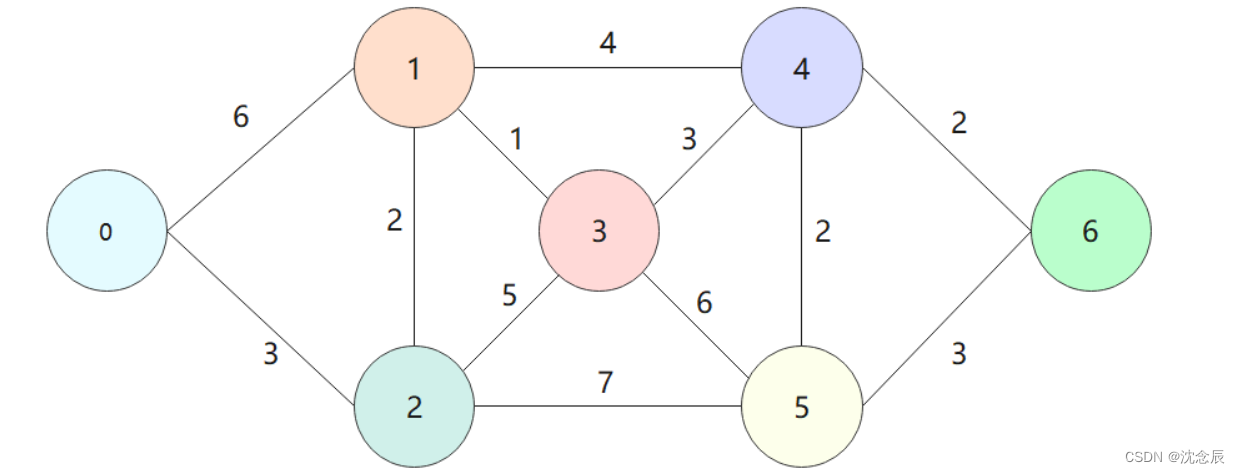
还是这个图，只不过这个算法更容易找的是任意两点之间的最短距离，我们需要先弄个2维数组，然后一个点一个点的去修改权重，最后得出结果，不过这个算法可以解决负权边的情况，这也是他的优点。（但是是真的蛮麻烦的，如果顶点多要累死）

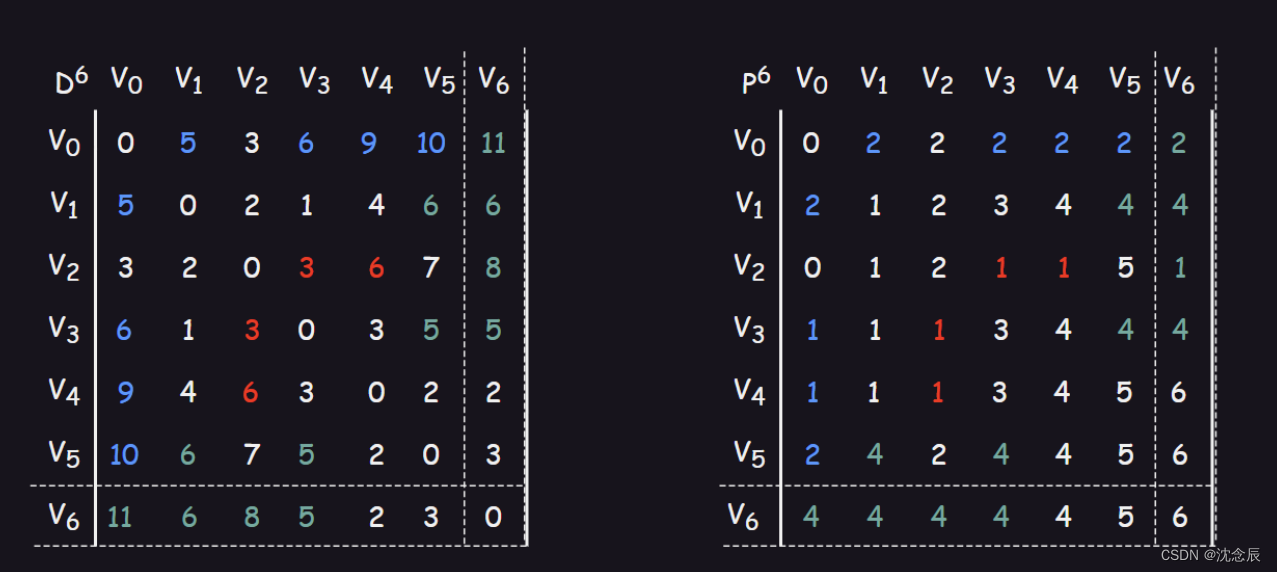
这是其他博主得出的结果，具体学习可以看他的这篇文章：图算法——求最短路径（floyd算法）

matlab代码

%在这个代码中，首先定义了一个带权有向图的邻接矩阵。然后，初始化到各个节点的距离。接着，运行floyd算法，计算出最短路径。最后，使用matlab的fprintf函数输出结果。
% 定义带权有向图
n = 5; % 节点数
adj_matrix = [0 10 inf 5 inf; inf 0 1 2 inf; inf inf 0 inf 4; inf 3 9 0 2; 7 inf 6 inf 0]; % 邻接矩阵

% 初始化
dist = adj_matrix;
for i = 1:n
    dist(i, i) = 0;
end

% 运行floyd算法
for k = 1:n
    for i = 1:n
        for j = 1:n
            if dist(i, k) + dist(k, j) < dist(i, j)
                dist(i, j) = dist(i, k) + dist(k, j);
            end
        end
    end
end

% 输出结果
fprintf('最短路径：\n');
for i = 1:n
    for j = 1:n
        if dist(i, j) == inf
            fprintf('inf\t');
        else
            fprintf('%d\t', dist(i, j));
        end
    end
    fprintf('\n');
end

三、a*算法

（说白了就是dijkstra算法plus版，只不过他是先找到最优点，省了时间）

a*算法是一种启发式搜索算法，用于在图形或网络中找到最短路径。它结合了dijkstra算法的广度优先搜索和启发式函数的评估，以提高搜索效率。

基本概念

1. 节点评估：每个节点都有一个估价函数，用于评估该节点到目标节点的距离。这个估价函数通常使用启发式函数来估计距离，例如曼哈顿距离或欧几里得距离。
2. 开放列表和关闭列表：a*算法使用两个列表来跟踪搜索过程中的节点。开放列表存储待扩展的节点，关闭列表存储已经搜索过的节点。
3. 估价函数和总代价：每个节点都有一个估价函数值，表示从起始节点到该节点的估计代价。总代价则是节点的估价函数值加上从起始节点到该节点的实际代价。
4. 启发式搜索：a*算法在扩展节点时，选择总代价最小的节点进行扩展。这样可以优先选择路径估计最优的节点，以期望更快地找到最短路径。
5. 路径重构：一旦找到目标节点，a*算法可以通过回溯父节点的方式，从目标节点开始重构最短路径。

a*算法通过下面这个函数来计算每个节点的优先级。

f ( n ) = g ( n ) + h ( n ) 

其中：

• f ( n )是节点n的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高（值最小）的节点。
• g ( n ) 是节点n距离起点的代价。
• h ( n ) 是节点n距离终点的预计代价，这也就是a*算法的启发函数。关于启发函数我们在下面详细讲解。

a*算法在解决图形搜索、迷宫问题、游戏ai等领域具有广泛应用。它在搜索过程中利用了启发式函数的启发性信息，能够快速找到最短路径，并且在启发式函数设计得当的情况下，可以保证找到最优解。

基本流程

1. 将起始节点加入开放列表，并设置其 g(n) 值为0。
2. 当开放列表不为空时，重复以下步骤：（开放列表就是放还没有走过的点，不为终点就可以找）
3. 从开放列表中选择 f(n) 值最小的节点 n。（即优先级最高的点）
4. 将节点 n 从开放列表中移除，并加入关闭列表。（说明这个点走过了）
5. 如果节点 n 是目标节点，算法终止，路径找到。
6. 对于节点 n 的所有相邻节点 m，执行以下操作：
7. 如果节点 m 不在开放列表和关闭列表中，将节点 m 加入开放列表，并计算它的 g(m) 和 h(m) 值。
8. 如果节点 m 已经在开放列表中，比较新的 g(m) 值与当前 g(m) 值的大小，选择更小的值作为 g(m)，并更新节点 m 的父节点为节点 n。
9. 如果节点 m 已经在关闭列表中，比较新的 g(m) 值与当前 g(m) 值的大小，选择更小的值作为 g(m)，并重新将节点 m 加入开放列表。

（执行算法的过程中，每个点需要记录达到该点的前一个点的位置 – 可以称之为父节点。这样做之后，一旦到达终点，便可以从终点开始，反过来顺着父节点的顺序找到起点，由此就构成了一条路径。）

个人理解

这个算法难就难在根据情况去设估价函数了，需要一个函数给每个点以及点之间的距离算出代价，然后根据算出的结果加快整个寻找最短路径的过程，有了整个估算，就照着算法的流程，从代价小的来就行。

具体学习可以参考这篇文章：a*算法（超级详细讲解）

matlab代码

这个代码需要自己定义一部分函数。

%需要根据具体问题和数据结构进行适当的修改和调整。代码使用了优先队列数据结构（priorityqueue），需要定义启发式函数（heuristicfunc）和节点邻接函数（adjacencyfunc），以适应具体问题。
function [path, cost] = astar(startnode, goalnode, heuristicfunc, adjacencyfunc)
    % 初始化open和closed列表
    openlist = priorityqueue();
    closedlist = containers.map();
    
    % 将起始节点添加到open列表
    openlist.insert(startnode, 0);
    
    % 初始化节点的代价和父节点
    gcost = containers.map();
    gcost(startnode) = 0;
    parent = containers.map();
    
    % 开始a*搜索
    while ~openlist.isempty()
        % 从open列表中选择代价最小的节点
        currentnode = openlist.extractmin();
        
        % 如果当前节点是目标节点，则构建路径并返回
        if currentnode == goalnode
            path = constructpath(parent, currentnode);
            cost = gcost(goalnode);
            return;
        end
        
        % 将当前节点添加到closed列表
        closedlist(currentnode) = true;
        
        % 获取当前节点的邻居节点
        neighbors = adjacencyfunc(currentnode);
        
        for i = 1:length(neighbors)
            neighbor = neighbors(i);
            
            % 如果邻居节点在closed列表中，跳过
            if iskey(closedlist, neighbor)
                continue;
            end
            
            % 计算从起始节点到邻居节点的代价
            tentativegcost = gcost(currentnode) + distance(currentnode, neighbor);
            
            % 如果邻居节点不在open列表中，或者新的代价更小
            if ~openlist.contains(neighbor) || tentativegcost < gcost(neighbor)
                % 更新邻居节点的代价和父节点
                gcost(neighbor) = tentativegcost;
                parent(neighbor) = currentnode;
                
                % 计算a*的估计总代价（f值）
                fvalue = gcost(neighbor) + heuristicfunc(neighbor, goalnode);
                
                % 将邻居节点添加到open列表或更新其代价
                if ~openlist.contains(neighbor)
                    openlist.insert(neighbor, fvalue);
                else
                    openlist.decreasekey(neighbor, fvalue);
                end
            end
        end
    end
    
    % 如果open列表为空，说明无法找到路径
    path = [];
    cost = -1;
end

function path = constructpath(parent, node)
    % 根据父节点构建路径
    path = [];
    while iskey(parent, node)
        path = [node path];
        node = parent(node);
    end
    path = [node path];
end

四、d*算法

d*（d-star）算法是一种增量式路径规划算法，用于在动态环境中更新和重新规划路径。它是 a* 算法的扩展，可以有效地应对环境状态的变化。

基本概念

1. 基于图的路径规划： d* 算法将路径规划问题抽象为一个有向图，图的节点表示位置或状态，图的边表示连接两个节点的可能移动或转换方式。
2. 状态和代价： 每个节点都有一个状态和对应的代价值。状态表示节点在环境中的位置或状态信息，代价值表示到达该节点的成本，通常使用距离或时间作为代价。
3. 开放列表和代价图：
   1. 开放列表（open list）存储待扩展的节点。
   2. 代价图（cost map）存储每个节点的当前代价值。
4. 局部更新： d* 算法通过局部更新操作来快速响应环境的变化。当环境发生变化时，只需要更新与变化相关的节点和边的代价，而不必重新计算整个路径。
5. 反向传播： d* 算法使用反向传播来更新路径和代价信息。通过从目标节点开始反向传播，沿着当前路径反向更新每个节点的代价值，使得路径适应环境变化。
6. 重规划： 当环境状态发生变化时，d* 算法会重新规划路径。它从起始节点开始，通过局部更新和反向传播逐步更新路径和代价信息，直到找到一条新的最短路径。

算法是一种基于启发式搜索的路径规划算法，它可以在动态环境中找到最短路径。与a算法不同，d算法是增量式的，也就是说，它可以在实时环境中对路径进行增量更新。d算法最初由sven koenig和maxim likhachev在2002年提出。

d算法的基本思想是：在一个有向图上，从起点到终点的最短路径必定是一系列连续的边，而不是一些离散的节点。因此，d算法不是从起点开始，而是从终点开始，不断向起点方向搜索路径，并根据环境的变化动态更新路径。

基本流程

1. 初始化：将终点作为当前节点，将起点的代价f(x)置为0。
2. 扩展节点：从当前节点开始向相邻节点搜索路径，计算路径的代价，更新相邻节点的代价和f(x)值。
3. 路径更新：如果某个节点的代价发生变化，就更新它的相邻节点的f(x)值，并将它们添加到路径列表中。
4. 重复步骤2和3，直到找到起点为止。

d算法的优势是它可以在动态环境中进行实时路径规划。当环境发生变化时，d算法可以从上一次路径的终点处重新开始搜索，避免了重新规划整个路径的开销。但是，d*算法的缺点是它需要在扩展节点时进行路径更新，这可能会导致算法的效率降低。

个人理解

如果我们在给机器人做路径规划，我们采用a*算法时，当机器人遇到一个小障碍物突然挡住了他正在前进的路，那他就需要重新算一遍a*，以此来找到最佳路径，而这很没有必要，d*算法的存在就是为了解决这个重复计算的问题，在最开始求出目标路径后，把搜索过程的所有信息保存下来，等后面碰到了先验未知的障碍物时就可以利用一开始保存下来的信息快速的规划出新的路径。所以说d*算法是可以应对动态环境的。

具体学习可以看这篇文章：d-star算法简介及相关思考

matlab代码

%请注意，上述代码仅为示例，你可能需要定义自己的getneighbors函数来获取节点的邻居，以及根据实际应用场景定义自己的cost和heuristic函数来计算代价和启发式值。
function [path] = dstar(start, goal, obstacles)
    % 初始化
    gscore = inf(size(obstacles));
    rhsscore = inf(size(obstacles));
    parent = zeros(size(obstacles));
    
    % 将起点添加到open列表
    open = priorityqueue();
    open.insert(start, heuristic(start, goal));
    gscore(start) = 0;
    rhsscore(start) = heuristic(start, goal);
    
    while ~open.isempty()
        % 获取open列表中具有最小估计总成本的节点
        currentnode = open.pop();
        
        % 如果当前节点是目标节点，则已找到路径
        if currentnode == goal
            path = reconstructpath(start, goal, parent);
            return;
        end
        
        % 更新当前节点的g值
        if gscore(currentnode) > rhsscore(currentnode)
            gscore(currentnode) = rhsscore(currentnode);
        else
            gscore(currentnode) = inf;
            updateneighbors(currentnode, gscore, rhsscore, parent, open, obstacles);
        end
    end
    
    % 如果open列表为空但仍未找到路径，则无法到达目标节点
    error('no path found!');
end

function updateneighbors(node, gscore, rhsscore, parent, open, obstacles)
    neighbors = getneighbors(node, obstacles);
    
    for i = 1:numel(neighbors)
        neighbor = neighbors(i);
        if neighbor ~= node
            rhsscore(neighbor) = min(rhsscore(neighbor), cost(node, neighbor) + gscore(node));
            if gscore(neighbor) > rhsscore(neighbor)
                gscore(neighbor) = rhsscore(neighbor);
                parent(neighbor) = node;
                open.insert(neighbor, heuristic(neighbor, goal) + gscore(neighbor));
            end
        end
    end
end

function path = reconstructpath(start, goal, parent)
    path = [goal];
    currentnode = goal;
    
    while currentnode ~= start
        currentnode = parent(currentnode);
        path = [currentnode, path];
    end
end

function cost = cost(node1, node2)
    % 计算从node1到node2的代价，可以根据实际应用场景自定义
    cost = 1;
end

function h = heuristic(node, goal)
    % 估计从node到goal的启发式值，可以根据实际应用场景自定义
    h = abs(goal(1) - node(1)) + abs(goal(2) - node(2));
end

五、rrt*算法

（快速搜索随机树）

基本概念

rrt*（rapidly-exploring random tree star）是一种用于路径规划的算法，它能够在高维、复杂的空间中找到最优路径。下面是关于rrt*的基本概念：

1. 树结构：rrt*使用树结构来表示搜索空间。树的节点表示搜索过程中的状态，边表示节点之间的连接关系。
2. 随机采样：rrt*通过随机采样在搜索空间中生成新的节点。这些采样点可以在整个搜索空间中随机选择，也可以根据目标位置的分布进行更加智能化的采样。
3. 连接节点：通过计算采样点与现有树中最近节点之间的距离，并在两个节点之间创建一条边，将采样点连接到树中。
4. 可达性检查：在连接节点之前，需要对两个节点之间的路径做可达性检查，以确保没有被障碍物或其他限制所阻挡。
5. 近邻节点：为了快速找到最近的节点，rrt*维护一个近邻节点集合。该集合可以根据节点之间的距离进行排序，以便更快地找到最近的节点。
6. 代价函数：rrt*引入了一个代价函数来评估路径的优劣。代价函数考虑了路径的长度和其他性能指标，帮助算法在搜索过程中找到更优的路径。
7. 重连节点：rrt*会定期检查树中的节点，尝试通过改变连接关系来改善现有路径。这样可以在不重新规划整个路径的情况下，通过局部优化来提高路径质量。
8. 目标达到：当搜索树中的节点越来越接近目标位置时，rrt*会终止搜索并返回最优路径。

rrt*算法通过不断扩展树结构和优化路径，使得搜索空间中的采样点趋向于目标，并找到最优路径。它在机器人路径规划、无人机路径规划等领域具有广泛应用。

基本流程

1. 初始化：
   1. 创建一个树，将起始位置作为树的根节点。
   2. 初始化其他参数，如目标位置、最大迭代次数等。
2. 迭代：
   1. 在每次迭代中，生成一个随机采样点（通常是在可行空间内随机选择的点）。
3. 节点选择：
   1. 从树中选择最近的节点，该节点将成为新采样点的父节点。
4. 节点扩展：
   1. 生成新节点，以使新节点与父节点之间的路径尽可能直接，通常是通过沿直线路径向新采样点前进一定距离。
   2. 确保新节点在可行空间内。
5. 连接检查：
   1. 检查新节点与父节点之间的路径是否与障碍物碰撞。如果路径与障碍物相交，需要重新选择新节点或采用其他策略。
6. 节点添加：
   1. 如果新节点通过了连接检查，则将新节点添加到树中，并建立与父节点的连接。
7. 路径优化：
   1. 对树中的节点进行代价优化。这涉及到计算从起始节点到新节点的代价，并与旧节点的代价进行比较。如果新节点的代价更低，就更新路径。
8. 目标检查：
   1. 检查新节点是否接近目标位置。如果是，则路径规划完成。
9. 迭代终止条件：
   1. 可以设置迭代终止条件，如达到最大迭代次数或规划超时。
10. 路径返回：
    1. 如果路径规划成功，从目标节点回溯到起始节点，构建最终路径。
11. 结束：
    1. 返回最终路径或报告无法找到路径，根据实际情况采取适当的行动。

请注意，rrt* 的关键特点之一是不断优化节点之间的连接，以寻找最优路径。这意味着随着迭代次数的增加，算法将收敛到全局最优路径（在无障碍情况下），并且具有渐近最优性和一致性的特点。此外，rrt* 可以在高维、复杂的环境中进行路径规划，并且适用于自主机器人导航等领域。

个人理解

后面这些算法难度较大，我也暂时没有理解透彻，后续学习清楚后会继续修改文章。

具体学习算法可以参考这两篇文章：【规划】rrt*算法图解、全局路径规划：图搜索算法介绍4​​​​​​​

六、lpa*算法

基本概念

lpa*（lifelong planning a*）算法是一种用于路径规划的增量式搜索算法，旨在解决动态环境中的路径规划问题。它是a*算法的改进版本，具有以下基本概念和特点：

1. 增量式搜索：lpa*是一种增量式搜索算法，它可以逐步构建路径规划并在需要时进行更新。这使得它适用于动态环境，其中障碍物的位置或代价可能随时间变化。
2. 代价地图：lpa*维护一个代价地图，其中每个节点都有一个代价值（cost）。这个代价值表示从起始节点到该节点的路径代价。初始时，只有起始节点的代价值为零，其他节点的代价值未知。
3. 双向搜索：lpa*同时从起始节点和目标节点执行搜索，以便在搜索过程中快速找到一条路径。这有助于提高路径规划的效率。
4. 代价更新：当障碍物移动或代价发生变化时，lpa*可以快速更新路径，以考虑新的信息。它只需要更新受影响的节点，而不需要重新计算整个路径。lpa*算法使用启发式函数来估计从当前节点到目标节点的代价。启发式函数可以是欧式距离、曼哈顿距离等。
5. 最优性保证：与a类似，lpa可以保证找到最短路径（最低代价路径），前提是代价函数满足一致性条件（admissible and consistent）。
6. 扩展节点：lpa*通过扩展具有最小代价的节点来构建路径。这些节点通常是距离起始节点最近的未扩展节点。
7. 替代路径：lpa*不仅寻找最佳路径，还保留备选路径信息。这有助于在需要时切换到替代路径，以适应环境变化或障碍物的出现。

总之，lpa算法是一种适用于动态环境下的路径规划算法，具有增量搜索、代价地图和最优性保证等特点。它可以用于自主机器人导航、自动驾驶车辆、游戏开发和其他需要实时路径规划的应用中。

基本流程

1. 初始化：设置起始节点的代价为0，其他节点的代价为无穷大。将起始节点加入优先级队列，并设置其优先级为起始节点的代价值加上启发式函数的值。
2. 循环直到找到路径或无法到达目标节点： a. 从优先级队列中取出优先级最高的节点。 b. 检查该节点是否已经更新过。如果已经更新过，则跳过该节点，继续下一轮循环。 c. 更新该节点的代价值为其父节点的代价值加上到达父节点的边的代价。 d. 如果该节点是目标节点，则找到了一条路径。结束算法。 e. 更新与该节点相邻的节点的代价值和优先级。如果更新了节点的代价值，将其加入优先级队列。
3. 结束：如果优先级队列为空而无法找到路径，则表示无法到达目标节点。

lpa*算法通过不断地选择和更新优先级队列中的节点，逐步优化代价值，直到找到一条到达目标节点的路径或者确定无法到达目标节点。在每次更新节点时，需要考虑节点的代价值和启发式函数的值来确定优先级。

个人理解

在a*的基础上，延伸到了动态环境，个人觉得，与d*lite算法蛮类似的，都是动态环境，都加入了启发函数。

具体学习可以参考这篇文章：lpa* 路径搜索算法介绍

python代码实现的文章：lpa* 路径搜索算法介绍及完整代码

七、d*lite算法

基本概念

dlite算法是一种路径规划算法，旨在解决在动态环境中的最短路径问题。它是对d算法的改进和优化。

d*lite算法的基本概念如下：

1. 初始化：首先，需要知道起始点和目标点。算法会根据当前的环境状态创建一个图，并将起始点设置为当前位置。
2. 估计代价：使用启发式函数来估计当前位置到目标点的代价。这个代价可以是直线距离、曼哈顿距离等。
3. 生成路径：根据启发式函数，选择具有最小估计代价的邻居节点作为下一个要访问的节点。然后，更新当前位置为选择的邻居节点，并将其添加到路径中。
4. 动态更新：如果有新的信息（例如，环境中的障碍物发生变化），d*lite算法可以根据这些信息动态更新路径。它会重新评估受到影响的节点，并相应地调整路径。
5. 迭代优化：重复执行生成路径和动态更新的步骤，直到找到从起始点到目标点的最短路径。

dlite算法的优点在于它能够在动态环境中实时更新路径，并能够处理障碍物的变化。这使得它在机器人导航、无人机路径规划等领域有着广泛的应用。如果你想深入了解dlite算法的实现细节和应用示例，我建议你查阅相关的学术论文和在线资源。

基本流程

1. 初始化起始点和目标点。
2. 估计当前位置到目标点的代价。
3. 选择邻居节点中具有最小估计代价的节点，并更新当前位置和路径。
4. 如果有新的信息，动态更新节点和路径。
5. 重复步骤3和步骤4直到找到最短路径。

个人理解

就是在d算法的基础上加了个和a*算法类似的启发函数，对当前情况进行评估，从而选出最优。

具体学习可以参考这篇文章：路径规划：d*lite寻路算法详解

八、各路径规划算法之间的区别（重要）

我们可以通过算法之间的区别来理解算法之间的关系

dijkstra算法对于带权图中任意两个节点之间的最短路径问题非常有效，但在大规模图和复杂环境中，由于需要搜索所有可达节点，其时间和空间复杂度较高。

为了解决dijkstra算法效率低的问题，a*算法作为一种启发式算法被提出。该算法在广度优先的基础上加入了一个估价函数。通过合理设计启发函数（估价函数），可以将搜索范围缩小到可能最佳路径周围的区域，从而大大减少搜索节点的数量。确保按照最小的总代价进行搜索。

（简单来说，dijkstra算法不错，但是节点多的时候，挨着搜还是太慢了，不如加个估价函数，然后先评估一下哪个地方可能最佳，直接缩小节点数量，提高效率，由此提出了a*算法）

当然，我们点与点之间的关系，不可能只有距离，有时还用一种权重去表示，这样，就有了负权边，负权边可以在某些特定情况下引入更复杂的问题，因为它们与正权边不同，可能会影响最短路径计算的结果。

对于一些最短路径算法，如dijkstra算法，其前提条件是边的权重必须为非负数。而floyd算法则可以处理带有负权边的图。

a*算法适用于在静态环境中搜索单源最短路径，但是环境是不停的变化的，比如说玩游戏的自动寻路，他不可能一直直着走，也会拐弯，需要避障，这是就提出了在动态环境下进行路径规划的d*算法。d*算法是增量式的，d算法不是从起点开始，而是从终点开始，不断向起点方向搜索路径，并根据环境的变化动态更新路径，但是，d*算法需要提前获取一条路径进行参考，并且在动态环境中需要实时响应变化，可能会受到计算和存储开销的限制。d*算法适用于在动态环境中进行路径重新规划。

但我们也能看出来，d*算法为了避障，每次更新都会遍历整个路径，可能导致较高的计算复杂度。对于大规模环境或频繁更新路径的情况，性能可能会有所下降。所以d*lite算法在d算法的基础上引入了启发式函数和优先队列，以减少不必要的计算量和提高搜索效率。通过使用与a*类似的启发式函数，d*lite算法能够更好地选择节点进行扩展，从而优化路径规划的质量和性能。

lpa*算法是基于a*算法的扩展，用于解决动态环境下的路径规划问题。它通过维护节点的当前代价值和参考代价值，以及一个更新列表，通过多次迭代搜索和增量更新策略来实现路径的快速更新。lpa算法和d*算法都是增量式路径规划算法，用于处理动态环境下的路径更新问题。相比于d*算法，lpa算法引入了参考代价值和更新列表，采用多次迭代搜索和增量更新策略，更加高效地进行路径更新。具体选择哪种算法应根据具体问题需求和环境特点进行评估。

rrt算法适用于在复杂、高维空间中的路径规划。

floyd算法适合找寻任意两点之间的最短路径。

最后总结

dijkstra算法（挨着搜太慢）——>a*算法（可以通过估价函数，找到最合适的点开始，但只能在静态环境）——>lpa*算法（可以在动态环境搜寻最短路径）

d*算法（可以在动态环境搜寻最短路径，但他也是遍历一遍，计算量太大）——>d*lite算法（加入和a*一样的估价函数，进行评估，更好地选择节点进行扩展​​​​​​​）

如有侵权，请联系删除，多谢！本文只作为学习经验分享，无盈利。