【神经网络】卷积神经网络CNN

卷积神经网络

欢迎访问blog全部目录！

1. 神经网络概览

leijnen, stefan & veen, fjodor. (2020). the neural network zoo. proceedings. 47. 9. 10.3390/proceedings47010009.

2.cnn（convolutional neunal network）

cnn的核心为使用卷积核对图像矩阵进行卷积运算（线性运算）！！！

2.1.学习链接

学习笔记：深度学习（3）——卷积神经网络（cnn）理论篇_cnn理论-csdn博客
【深度学习】一文搞懂卷积神经网络（cnn）的原理（超详细）_卷积神经网络原理-csdn博客

2.2.cnn结构

2.2.1.基本结构

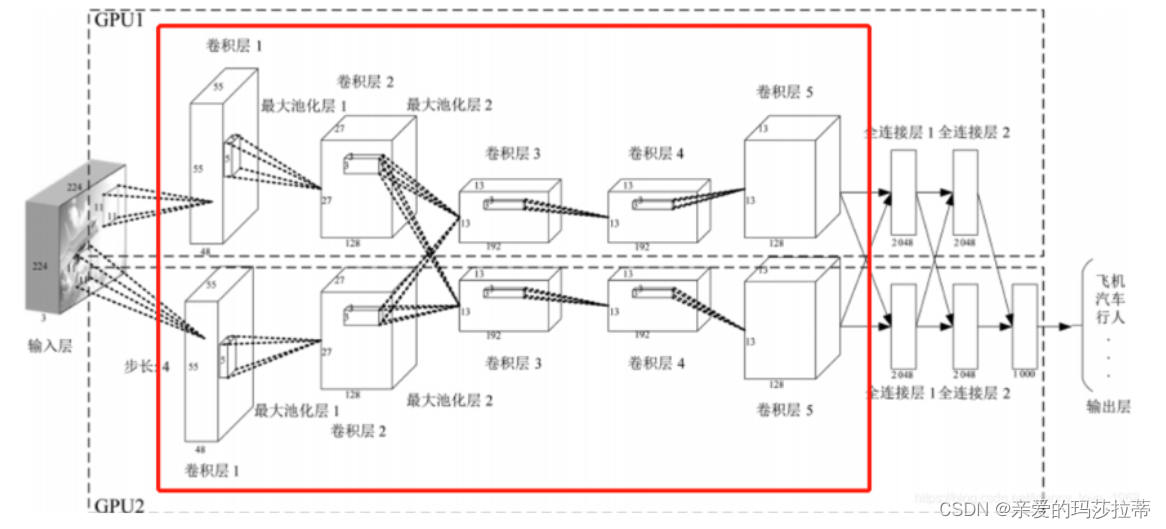
2.2.1.1输入层

​ 图片在计算机中是包括 （宽，高，深）的三维矩阵，元素为灰度值或rgb值，其中矩阵的深即为rgb层次。如果为rgb图片，图片深度为3。图片的三维矩阵即为cnn的输入。（宽，高）矩阵为1个channel，（宽，高）矩阵为特征图。

​ 输入层即接收原始图片数据，cnn可以保留图片的连续像素（物体的不变性），加深神经网络对图片的理解。

2.2.1.2.卷积层|convolution layers

作用：捕捉图片的局部特征而不受其位置的影响。

多个卷积核叠加即为卷积层。

卷积层后需接激活函数（如relu）来引入非线性。

2.2.1.3.池化层|pooling layers

作用：通过减小特征图的大小（下采样）来减少计算复杂性。它通过选择池化窗口内的最大值或平均值来实现。这有助于提取最重要的特征。

有点类似于图像的模糊处理！

2.3.1.4.全连接层|linear layers

全连接层将提取的特征映射转化为网络的最终输出。这可以是一个分类标签、回归值或其他任务的结果。

2.2.2.核心要素

名称	name	含义
过滤器（卷积核）		过滤器为可移动的三维小窗口矩阵（n*n*n）【kernel_size】，它是一组固定的权重。卷积操作即为将卷积核与图像进行逐元素相乘后相加。
步长	stride	卷积核每次滑动位置的步长。
卷积核的个数	out_channels	决定输出矩阵的深度depth。一个卷积核输出一个深度层。
填充值	zero-padding	在外围边缘补充若干圈0，方便从初始位置以步长为单位可以刚好滑倒末尾位置。数据填充的主要目的是确保卷积核能够覆盖输入图像的边缘区域，同时保持输出特征图的大小=输入特征图大小。 如果想要维持特征图大小不变，$padding=(kernel\_size-1)/2$！！

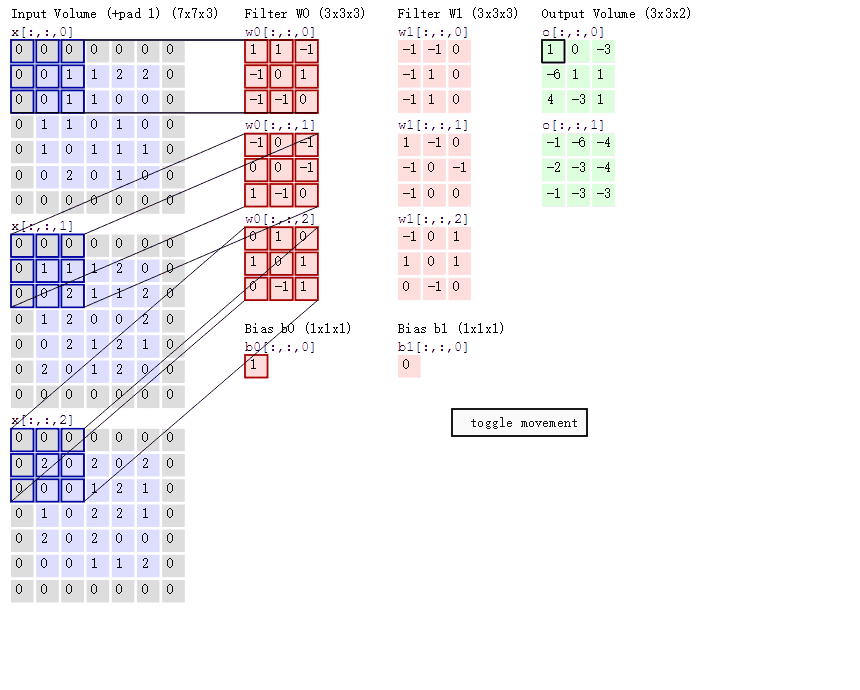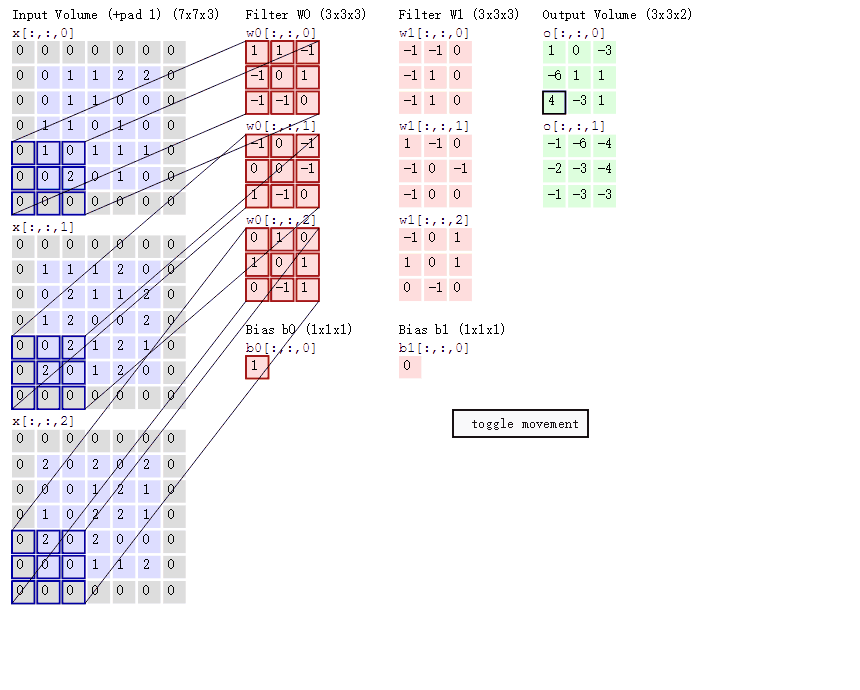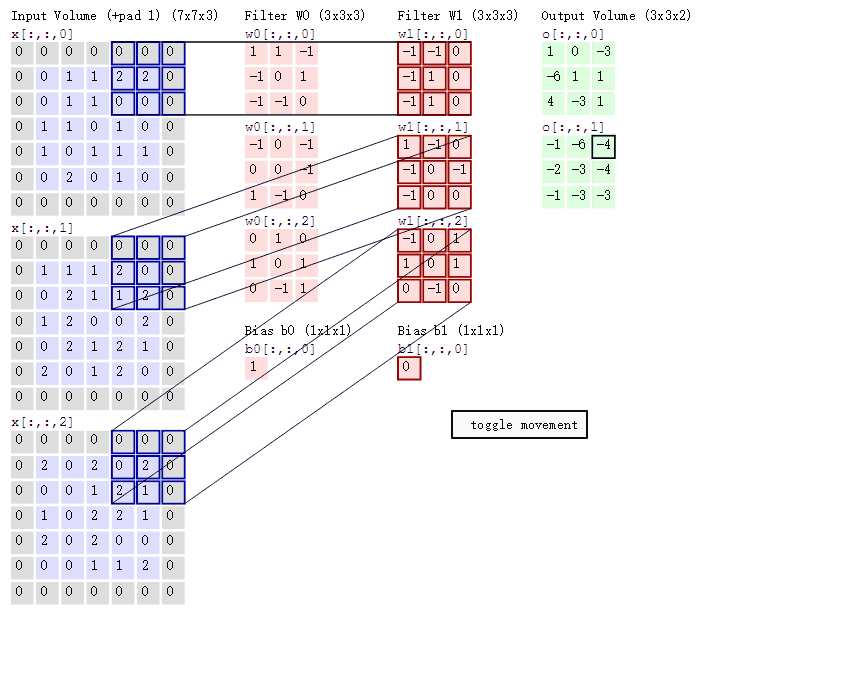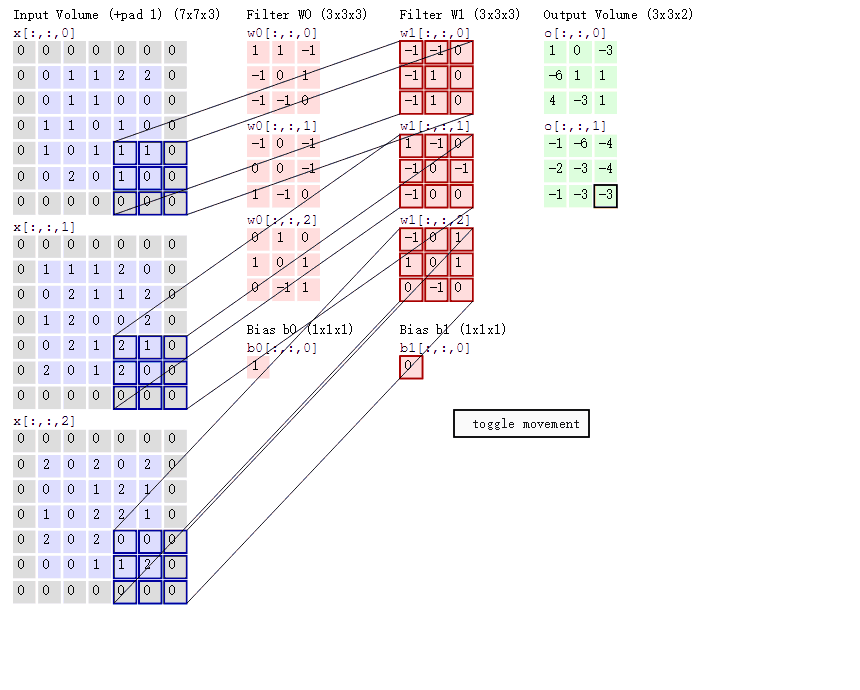
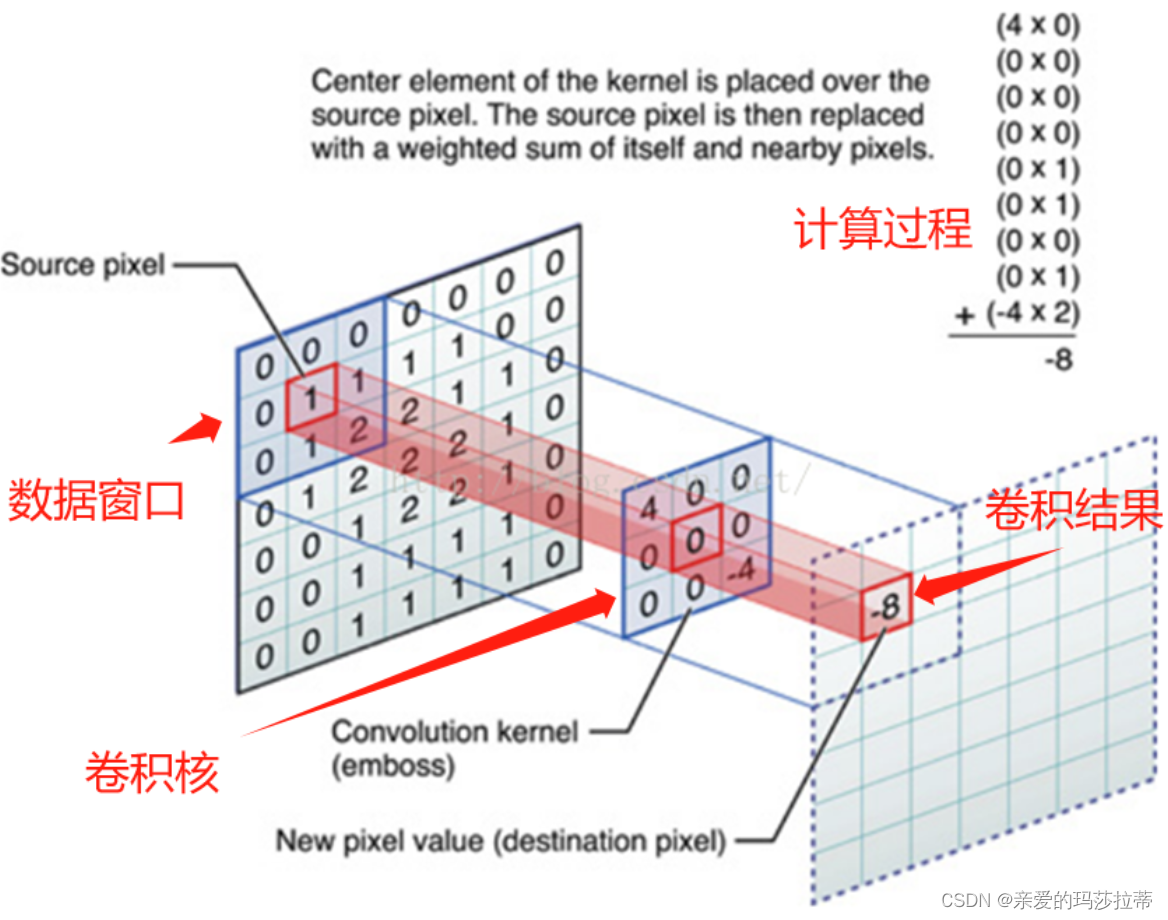
以下图为例(图示为conv2d)：

步长=2，卷积核个数=2，填充值=1（在图片周围补1圈0），卷积核尺寸为3*3*3

2.3.pytorch cnn

api：torch.nn.convolution-layers — pytorch 2.2 documentation

2.3.1.区分conv1d与conv2d

	conv1d	conv2d
输入	语音：二维矩阵	图像：三维矩阵
卷积核	（卷积核尺寸（二维），卷积核个数）	（卷积核尺寸（三维），卷积核个数）
总结	在特征图内只能竖着扫	在特征图内先横着扫再竖着扫

图像的cnn使用的是conv2d！！

2.3.2.cnn搭建与参数

import torch
import torch.nn as nn

class cnn(nn.module):
    def __init__(self):
        super(cnn, self).__init__()
        self.conv1 = nn.sequential(  # 输入图像尺寸为(1，28，28)
            nn.conv2d(
                in_channels=1,  # 输入图像的深度 灰度图为1，rgb图为3
                out_channels=16,  # 卷积核个数，输出图像的深度
                kernel_size=5,  # 卷积核尺寸5*5*1
                stride=1,  # 步长
                padding=2  # 填充大小 如果想要 con2d 出来的图片长宽没有变化, padding=(kernel_size-1)/2
            ),  # 输出图像尺寸为(16,28,28)
            nn.relu(),  # 激活函数
            nn.maxpool2d(
                kernel_size=2,  # 池化小区域尺寸2*2，区域模糊
                # stride=2,  # 步长，默认=kernel_size
            ),  # 输出图像尺寸为(16,14,14)
        )
        self.conv2 = nn.sequential(  # 输入图像尺寸为(16,14,14)
            nn.conv2d(
                in_channels=16,  # 输入图像的深度
                out_channels=32,  # 卷积核个数，输出图像的深度
                kernel_size=5,  # 卷积核尺寸5*5*16
                stride=1,  # 步长
                padding=2  # 填充大小
            ),
            nn.relu(),
            nn.maxpool2d(
                kernel_size=2,
            )  # 输出图像尺寸为(32,7,7)
        )
        self.out = nn.linear(32 * 7 * 7, 10)  # 输出10*1的矩阵

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        # x图像平铺成 (batch_size=1, 32 * 7 * 7)
        x = x.view(x.size(0), -1)  # view中一个参数定为-1，代表自动调整这个维度上的元素个数，以保证元素的总数不变。
        output = self.out(x)
        return output


cnn = cnn()
print(cnn)
'''
cnn(
  (conv1): sequential(
    (0): conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (1): relu()
    (2): maxpool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=false)
  )
  (conv2): sequential(
    (0): conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (1): relu()
    (2): maxpool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=false)
  )
  (out): linear(in_features=1568, out_features=10, bias=true)
)
'''

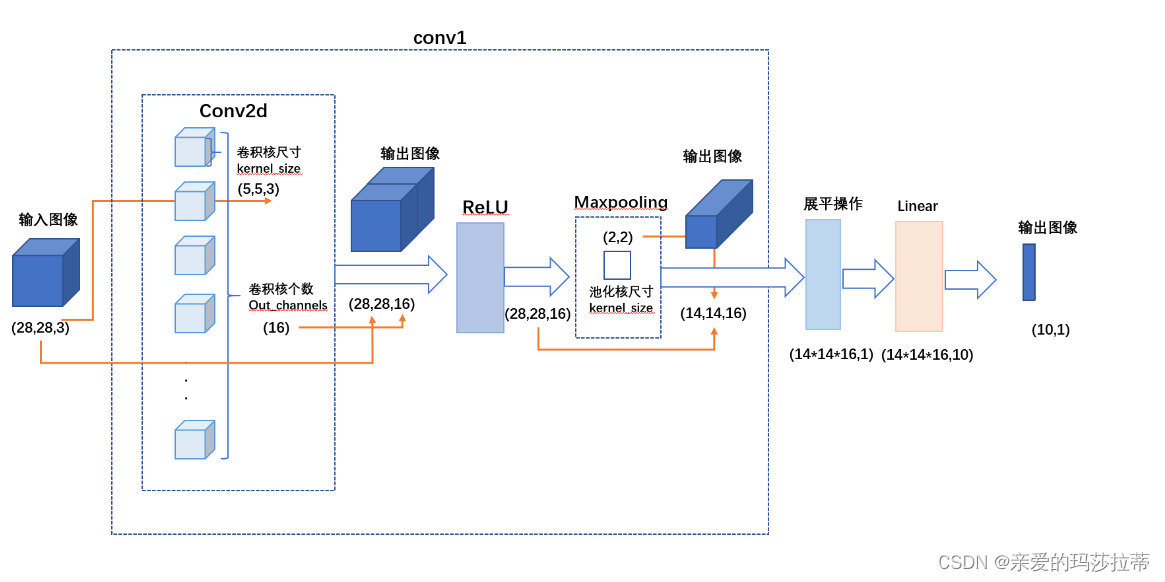
2.3.3.示意图⭐️

注：由于画幅有限，示意图仅画了1个大卷积层。