【机器学习】深入理解损失函数(Loss Functions)

---

🌈个人主页: 鑫宝code
🔥热门专栏: ｜ 炫酷html | javascript基础
​💫个人格言: "如无必要，勿增实体"

---

深入理解损失函数(loss functions)

在机器学习和深度学习领域,损失函数(loss function)扮演着至关重要的角色。它是用于衡量模型预测值与真实值之间差距的一种度量标准,也是优化算法最小化的目标函数。选择合适的损失函数对于训练出高质量的模型至关重要。本文将深入探讨损失函数的基本概念、常见类型及其应用场景,帮助读者更好地理解和应用损失函数。

什么是损失函数?

在监督学习任务中,我们通常会构建一个模型来预测输入数据的目标值。模型的输出值通常会与真实的目标值存在一定差距,这种差距就是我们所说的"损失"(loss)。损失函数的作用就是对这种差距进行量化,将其转化为一个可计算的数值。

具体来说,损失函数是一个函数,它接受模型的预测值和真实值作为输入,输出一个非负实数,表示预测值与真实值之间的差距程度。我们的目标是找到一个模型,使得其在训练数据和测试数据上的损失函数值最小。

数学上,我们可以将损失函数表示为:

$$l(y,y_i)$$

其中,y表示真实值,y_i表示模型的预测值,l是损失函数。

在训练过程中,我们通常使用优化算法(如梯度下降)来最小化损失函数,从而找到模型的最优参数。因此,选择合适的损失函数对于模型的性能至关重要。

常见损失函数类型

根据任务的不同,我们可以选择不同类型的损失函数。以下是一些常见的损失函数类型:

1. 均方误差(mean squared error, mse)

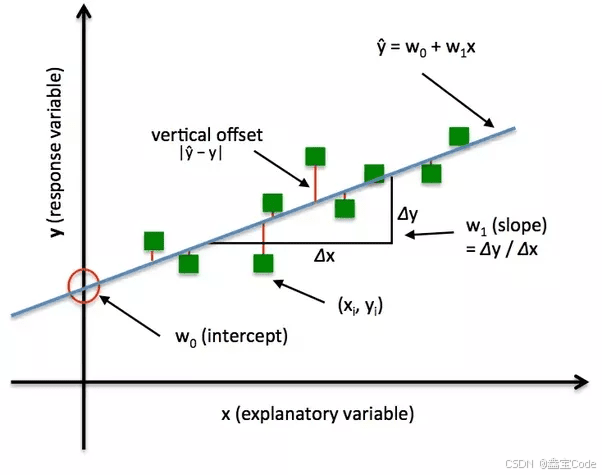
均方误差是一种常用的回归任务损失函数,它计算预测值与真实值之间的平方差的均值。数学表达式如下:

$$mse=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

其中,n是样本数量。

均方误差对于异常值比较敏感,因为它对于大的误差给予了更大的惩罚。它常用于线性回归等回归任务中。

2. 交叉熵损失(cross-entropy loss)

广泛应用于分类任务，特别是多类和二分类问题。它衡量概率分布之间的差异，鼓励模型预测的概率分布与真实标签尽可能一致。

$$ce=-\frac{1}{n}\sum _{i=1}^n\sum _{c=1}^c{t}_{ic}\log (p_{ic})$$
其中$t_{ic}$ 是第 $i$ 个样本属于第 $c$ 类的真实标签（one-hot编码），$p_{ic}$ 是模型预测的概率。

交叉熵损失在深度学习中被广泛使用,因为它可以直接优化模型输出的概率分布,而不需要进行额外的转换。

3. 铰链损失(hinge loss)

铰链损失常用于支持向量机(svm)中,它衡量了样本到决策边界的距离。铰链损失的公式如下:

$$\text{hinge}=\max (0,1-t\cdot y)$$

其中 𝑡 是真实标签（-1 或 +1），𝑦 是模型预测的原始输出。
铰链损失的优点是它对于远离决策边界的样本不会给予过多惩罚,这有助于svm找到一个具有最大间隔的决策边界。

4. huber损失(huber loss)

huber损失是均方误差和绝对误差的一种组合,它在一定程度上结合了两者的优点。huber损失的公式如下:

$$l_{\delta }(r)=\{\begin{array}{ll}\frac{1}{2}{r}^2& \text{if }|r|\le \delta \\ \delta (|r|-\frac{1}{2}\delta )& \text{otherwise}\end{array}$$

其中,delta是一个超参数,用于控制损失函数在均方误差和绝对误差之间的转换点。

huber损失对于小的误差使用均方误差,对于大的误差使用绝对误差,这样可以在一定程度上避免异常值的影响,同时保持对于小误差的敏感性。

5. 焦点损失(focal loss)

焦点损失（focal loss）是一种专为解决类别不平衡问题而设计的损失函数，最初在目标检测领域被提出，但在其他分类任务中也得到了广泛应用。focal loss旨在解决深度学习模型中常见的正负样本比例严重失衡的问题，通过降低易分类样本的权重，使得模型更加关注那些难分类的样本，从而改善模型的分类性能。

$$l_{fl}(y,p)=-{\alpha }_t(1-p_t{)}^{\gamma }\log (p_t)$$

其中 ${\alpha }_t$和 $p_t$ 的具体值取决于 $y$ 的值。焦点损失通过引入这两个调节因子，有效地解决了类别不平衡问题，提高了模型对少数类的识别能力。

损失函数的选择策略

选择合适的损失函数对于模型的性能至关重要。以下是一些选择损失函数的策略:

1. 根据任务类型选择:不同的任务类型通常需要使用不同的损失函数。例如,回归任务通常使用均方误差或绝对误差,分类任务通常使用交叉熵损失或铰链损失。

2. 考虑数据分布:如果数据存在异常值或噪声,我们可以选择对异常值不太敏感的损失函数,如huber损失。如果存在类别不平衡问题,可以考虑使用焦点损失等。

3. 结合任务目标:除了预测准确性之外,我们还需要考虑任务的其他目标。例如,在目标检测任务中,我们可能希望模型能够更好地定位目标边界,因此可以使用一些专门设计的损失函数,如iou损失等。

4. 实验比较:对于同一个任务,我们可以尝试使用不同的损失函数,并比较它们在验证集上的表现,选择效果最好的那个。

5. 组合损失函数:在某些情况下,我们可以将多个损失函数进行加权组合,以结合它们各自的优点。例如,我们可以将均方误差和绝对误差进行加权组合,以获得更好的性能。

总的来说,选择合适的损失函数需要结合具体任务、数据特点和目标进行综合考虑。在实际应用中,我们可以先根据经验选择一个初始损失函数,然后通过实验比较和调整来寻找最佳的损失函数。

自定义损失函数

除了使用现有的损失函数之外,我们还可以根据具体需求自定义损失函数。自定义损失函数的过程通常包括以下几个步骤:

1. 明确任务目标:首先,我们需要明确自己的任务目标是什么,例如提高预测准确性、加强模型的鲁棒性等。

2. 分析现有损失函数的局限性:接下来,我们需要分析现有损失函数在达成任务目标方面的局限性,找出它们的不足之处。

3. 设计新的损失函数:根据任务目标和现有损失函数的局限性,我们可以设计出一种新的损失函数,以更好地满足任务需求。

4. 实现和测试:将新的损失函数用代码实现出来,并在实际数据集上进行测试和评估,观察它是否能够达到预期效果。

5. 调整和优化:如果新的损失函数的效果不理想,我们可以对它进行调整和优化,例如调节超参数、与其他损失函数进行组合等。

6. 理论分析:最后,我们可以对新的损失函数进行理论分析,探讨它的数学性质、收敛性等,为将来的应用提供理论支持。

自定义损失函数的过程需要一定的创新性和实践经验,但它可以帮助我们更好地解决特定任务,提高模型的性能。在深度学习领域,许多新的损失函数都是通过这种方式设计出来的。

损失函数的发展趋势

随着机器学习和深度学习技术的不断发展,损失函数也在不断演进和创新。以下是一些损失函数的发展趋势:

1. 任务特定损失函数:随着任务的不断细分和专门化,我们需要设计出更多针对特定任务的损失函数,以更好地满足任务需求。例如,在图像分割任务中,已经出现了一些专门的损失函数,如dice loss、tversky loss等。

2. 注重模型解释性:除了预测准确性之外,我们还需要关注模型的解释性和可解释性。因此,一些新的损失函数被设计出来,以提高模型的可解释性,例如信息理论损失函数等。

3. 引入先验知识:一些新的损失函数试图将人类的先验知识融入其中,以提高模型的性能和鲁棒性。例如,在自然语言处理任务中,我们可以设计出一些融入语言学知识的损失函数。

4. 端到端训练:随着端到端训练范式的兴起,我们需要设计出能够支持端到端训练的损失函数,以避免传统的多阶段训练过程。

5. 组合损失函数:未来可能会出现更多组合多个损失函数的方法,以结合它们各自的优点,获得更好的性能。

6. 元学习损失函数:利用元学习的思想,我们可以尝试自动学习或优化损失函数本身,而不是手动设计。

总的来说,损失函数的发展趋势是朝着更加任务特定、更加解释性强、更加智能化的方向发展。随着新技术和新需求的不断出现,损失函数的创新也将不断推进。

总结

本文详细介绍了损失函数的基本概念、常见类型及其应用场景,并探讨了如何选择和自定义损失函数,以及损失函数的发展趋势。损失函数是机器学习和深度学习中一个非常重要的概念,它直接影响着模型的性能和质量。选择合适的损失函数需要结合任务目标、数据特点和实践经验进行综合考虑。同时,我们也可以根据具体需求自定义新的损失函数,以更好地满足特定任务的需求。

未来,随着技术的发展和新需求的出现,损失函数将继续演进和创新,以提供更好的性能、更强的解释性和更智能化的优化方式。相信通过不断的探索和实践,我们一定能够设计出更加优秀的损失函数,推动机器学习和深度学习技术的进一步发展。